Module Theory, Part II: Generation of Modules, Direct Sums, and Free Modules

September 15th, 2017

Definition: Let $R$ be a ring with identity, and $N_1, \dots,N_n$ are modules over $R$. Then:

$N_1 + \dots +N_n$ consists of all finite sums of elements ${n_1 + \dots + n_n}$ so that $n_i \in N_i$.
For any subset $A$ of $M$ let $RA = {r_1a_1 + \dots + r_na_n}$ so that $r_i \in R$, $a_i \in A$ and $m \in \mathbb{Z}$. By convention, if $A = \emptyset$ then we define $RA = {0}$. Indeed if $A = {a_1,\dots,a_n}$ then we can write $RA = Ra_1 + \dots + Ra_n$ and say that $RA$ is the submodule generated by $A$.
A submodule $N$ of $M$ is finitely generated if there is some finite subset $A$ of $M$ so that $N=RA$.
A submodule $N$ is cyclic if $N=Ra$ for some element $a\in M$.

Note that if $R$ has identity, then $RA=A$.

Examples

For a $\mathbb{Z}$-module, modules generated by $A\subset M$ are just subgroups generated by $A$.
A ring $R$ with identity is a cyclic module generated by $1$. Any submodule is an ideal. In particular, a submodule which is cyclic is exactly a principal ideal. In particular, a PID is just a (commutative) integral domain with identity so that every $R$-submodule of $R$ is cyclic.
Let $F$ be a field and consider an $F[x]$ module $V$, which is identified with the action of $x$. Then to say that $V$ is a cyclic $F[x]$-module is spanned by:

$$ \{v, T(v), T^2(v), \dots\} $$

For some $v\in V$ as a vector space over $F$.

Definition: Let $M_1, \dots, M_k$ be a collection of $R$-modules. Then we define the direct product:

$$ M_1 \times \dots \times M_k $$

Which consists of all the $k$-tuples of the modules, and it is clearly also an $R$-module. With a finite number $k$, we say that the direct sum $M_1 \oplus \times \oplus M_k$ is their direct product.

Proposition

TFAE:

The map $\pi: N_1 \times \dots \times N_k \rightarrow N_1 + \dots + N_k$ is defined by $\pi: (a_1,\dots,a_k) \mapsto a_1 + \dots + a_k$. $\pi$ is an isomorphism.

$N_j \cap (N_1 + \dots +N_{j-1} + N_{j+1}+\dots N_k) = 0$ for any choice of $j$.

Every $x \in N_1 + \dots + N_k$ can be written uniquely as $a_1 + \dots + a_k$ for $a_i \in N_i$.

Definition: An $R$-module $F$ is called free on the subset $A$ of $F$ if for every nonzero $x\in F$, there exist unique nonzero elements $r_1,\dots,r_n \in R$ so that:

$$ x = r_1a_1 + \dots r_na_n $$

And in this case, we say that $A$ is a basis or a set of generators for $F$. If $R$ is a commutative ring, the size of $A$ is called the rank of $F$.

An important distinction here is that $r_i$ as well as $a_i$ are unique, whereas in a direct sum only $a_i$ are unique.

Theorem

For any set $A$ there is a free $R$-module $F(A)$ on the set $A$. If $M$ is any $R$-module and $\varphi: A\rightarrow M$ a set map, then there is a unique module homomorphism $\Phi$ so that the following diagram commutes (where $j$ denotes the inclusion of $A$ into $F(A)$).

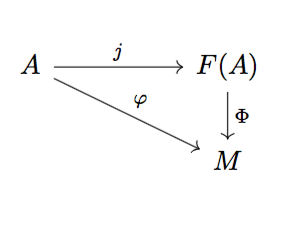
When $A$ is a finite set, we simply define $F(A) = Ra_1 \oplus \dots \oplus Ra_n \cong R^n$ (if $R$ has identity).

The proof is as follows. First, let $F(A) = {0}$ if $A=\emptyset$. Otherwise, let $F(A)$ be the set of all (set) functions $f:A \rightarrow R$ so that $f(a) = 0$ for all but finitely many $a$.

Indeed, we can see $A$ as being included in $F(A)$ by constructing the function $f_a$ such that $f_a(a)=1$ and $f_a(b)=0$ for all $b\neq a$. In this way, we can think of $F(A)$ as all (finite) linear combinations of elements of the form $f_a$ which can be identified with the elements of $A$. And indeed $F(A)$ has a unique expression as such a formal sum. This is a module in the obvious way.

Now, suppose that $\varphi(A)$ is a map from the set $A$ into an $R$-module $M$. Then we can define a map $\Phi: F(A) \rightarrow M$ by:

$$ \varphi: \sum\limits_{i=1}^n r_ia_i \mapsto \sum\limits_{i=1}^nr_i \varphi(a_i) $$

Since elements of $F(A)$ have unique representations in this form, this map is well-defined. And by definition, restricting $\Phi$ to $A$ yields exactly $\varphi$ as a module homomorphism. And $\Phi$ is unique because it must respect the module homomorphism axioms.

When $A$ is the finite set ${a_1,\dots,a_n}$, then we have that $F(A) = Ra_1 \oplus \times \oplus Ra_n$. And indeed we can say that $R\cong Ra_i$ under the map $r \mapsto ra_i$. Therefore, the free $R$-module of a set of size $n$ is simply $R^n$ (in a sense, the “simplest” module).

Corollary

If $F_1, F_2$ are free modules over $A$ there is a unique isomorphism between them which is the identity on $A$.

If $F$ is any free $R$-module with basis $A$, then $F \cong F(A)$.

This is essentially the statement that universal objects are unique.

Download this Page as a PDF:

Note: Images are replaced by captions.

Link to PDF

Jay Havaldar