The Amazing True Story Of The Quintic Formula
July 2nd, 2017
Behind every centuries-long intractable math problem, there’s a centuries-long list of great men and women who tried to solve it. These are stories you never really hear about in school, but looking at the people behind these breakthroughs often gives us incredible insight into some interesting and very human stories. In this post, I’m going to be talking about one problem in particular.
We all know the quadratic formula:
$$x = \frac{-b\pm \sqrt(b^2 + 4ac)}{2a}$$
For any quadratic polynomial, we can use this formula to find its roots. The same is true for cubic equations and quartic as well, although as we’ll get to, it’s not quite as simple. But a remarkable thing happens for polynomials of degree $5$ or over: there is no formula. Understanding why takes quite a bit of math, and the story of its development spans $250$ years. We’ll start this one like any other story: at the beginning.
Note that I’m a math guy and not a historian; if you’re interested in more details, you should probably check a more reliable source.
The Renaissance
The story starts in Italy during the late 1400s. It was a pretty peaceful time in Italy, especially in Florence, which was ruled by the famous Medici family. The Medicis were patrons of the arts, and were responsible for the likes of Leonardo da Vinci, Botticelli, and Michelangelo, among many others. Most historians mark Florence around this time as the birthplace of the Renaissance. Along with many achievements in art and philosophy, it was also the time of a lot of revolutionary math.

Unfortunately, this peace did not last very long. Starting in 1494, there was a series of conflicts all around northern Italy known as the Italian Wars, during which the Medici dynasty collapsed. As a result, Florence reshaped itself as a far more liberal state, and one which truly embraced the Renaissance. The Italian wars continued to ravage the region throughout the century, and at some point the various Italian states had no choice but to enter under the protection of the Holy Roman Empire. Ironically, this is exactly what the Renaissance needed, as with this increased security, the city of Venice in particular was able to blossom into an incredibly wealthy and liberal state, like Florence before it. If you’ve ever read The Merchant of Venice by Shakespeare, you have a general idea of what Venice looked like at the time.
These conditions are what allowed math to fluorish in the region at the time, and it was allowed two Italian mathematicians to solve a problem that was previously considered unsolvable by Indian, Chinese, and Islamic mathematicians: the solution of the cubic equation.
Math: A Dangerous Game
Believe it or not, math was a dangerous game at the time. There was a fairly common practice of mathematicians publicly challenging one another, and these were basically the math equivalent of duels. In a challenge, each mathematician must solve a problem suggested by the other, and the loser often lost funding or even their jobs. Stakes were fairly high, so there are a few instances of mathematicians publishing their greatest ideas only to a small group of trusted friends.
Cardano & Tartaglia
We start getting into the math with Gerolamo Cardano, the illegitimate child of Fazio Cardano (a close friend of none other than Leonardo da Vinci). He was unwanted by his parents and his siblings died from the Plague, so he had a pretty rough childhood (to say the least). His difficult upbringing is likely what led to his eccentric and often combative personality. Nonetheless, this guy influenced the likes of Newton, Leibniz, and Gauss with his ideas, and grew to be one of the greatest mathematicians of his era (and also a physician, writer, chemist, and gambler). He was even able to correctly predict the date of his own death! (This may be less impressive when you consider that he committed suicide)

Cardano was known for his short temper and belligerent attitude, and perhaps this is the reason why he was short on funds for most of his adult life. Although he successfully completed medical school, he was unable to find work afterwards due to his disagreeable personality. To make ends meet, the man took up gambling. Luckily, he was a mathematician, and so this wasn’t a bad gig at the time. Through his gambling he was able to study probability and use it to his advantage, ultimately writing multiple papers on the subject.
One of the major ideas in Cardano’s mathematical work was the first systematic use of negative numbers. Cardano even acknowledged imaginary numbers, although he didn’t have too sophisticated of an understanding of them (deeming them “useless”). As you can imagine, this was a pretty explosive time for discoveries in algebra. Arguably Cardano’s most famous work, however, began when he came across fellow mathematician Niccolò Fontana Tartaglia.
“Tartaglia” is Italian for “The Stammerer”, and Fontana was so named after an incident when French soldiers invaded his town during the Italian Wars. Hungry for revenge, the French decided to massacre the population of Brescia upon finally defeating their militia. A soldier eventually found the young Tartaglia (who was hiding in a cathedral), sliced his jaw, and left him for dead. He could never really talk properly again, so he embraced his nickname of “The Stammerer”.

Though Tartaglia was poor and self taught (reportedly he only learned half the alphabet from a private tutor before funds ran out), he was one of the most important thinkers of his era. He was the first to translate Euclid’s Elements into a modern European language, fixing a number of errors in the existing translations. Later on, Galileo (also an Italian) made extensive use of this translation.
Quick aside: Euclid’s Elements is one of the founding works of geometry from the ancient Greeks, and it is impossible to overstate how important it was to math. I even know of a few professors and mathematicians who assign their students to read the original Euclid text, to this day – it is maybe not the best way to learn geometry, but it definitely is the best insight into Euclid’s massively impactful way of thinking.
Tartaglia was able to sustain himself by moving to Venice and becoming a bookkeeper. There, he found a thriving intellectual environment where he could evolve as a mathematician and thinker. Remember that Venice was thriving at the time, and so while Tartaglia struggled for money, things could have been a lot worse for him at the time.
Where “The Stammerer” factors into our story is his achievements in algebra; Tartaglia was the first to solve the cubic equation in general (or so he thought).
Tartaglia’s Solution of the Cubic
Although Tartaglia believed he was one of the first to solve the cubic equation (and this was the widespread belief at the time), fellow Italian Scipione del Ferro solved the problem independently some decades earlier. However, due to the threat of public challenges from other mathematicians (which were especially famous at his workplace of the University of Bologna), Ferro never published his results before he died – but he did give his notebook to his son-in-law, a fellow mathematician. Of note here is that the University of Bologna is the oldest university in continuous operation, and it has been operating for 929 years at the time of this writing. Dante, Petrarch, Albrecht Durer, two Popes, and the guy who invented the radio all went there. It is likely that a few of Ferro’s (distinguished) colleagues at the university knew about the solution, but one would assume that none of them could duplicate it. At least one person is confirmed to have known about Ferro’s findings, his student Antonio Maria Fior.
Fior was poor and this is likely what led him to eventually challenge Tartaglia in 1535. Ferro did not tell his student how to solve any cubic, only equations of the form $x^3+ax=b$. Note that negative numbers were not widely used at the time (earlier, we talked about how this gave Cardano a crucial edge), so this really left quite a few cases unsolvable for Fior. Nonetheless, Fior was confident he could beat Tartaglia, and the two challenged each other with thirty problems each. Now, Tartaglia could solve cubics in some cases, but So, Fior challenged Tartaglia with thirty questions of this type (betting on Tartaglia solving only a few of them at best), while Tartaglia came up with thirty questions on a wide area of topics.
In the early morning on February 13th, 1535, Tartaglia solved the problem. He solved all thirty of the problems in 2 hours, and the winner was decided. Tartaglia did not take his prize; the honor of winning was enough for him.

Stories like this make me wonder if the world wouldn’t be better off if we brought back these high-stakes math challenges. After all, it was one of these challenges that allowed Tartaglia to come up with his partial solution in the first place. Hit me up by email if you want to challenge me, maybe we’ll solve some cool problems.
When Cardano heard of Tartaglia’s solution to the cubic (and when he realized that, brilliant as he was, he could not solve it himself), he wrote to the young Venetian asking him his method. Keep in mind that at the time, his colleagues had told Cardano that finding a solution was impossible, and it’s not hard to see why one would believe it. After all, the solution to the quadratic equation had been known to at least the ancient Greeks, Egyptians, Indians, and Chinese, and probably the Mayans before them (not that they would have known this at the time). If the problem had remained unsolved for millennia, what reason would Cardano have to believe he could solve it?
Tartaglia refused, which infuriated Cardano (remember, he was an incredibly short-tempered man). So Cardano wrote back, on the one hand instigating a challenge, but on the other offering to introduce the poor Tartaglia to one of his wealthy patrons. Although Cardano and Tartaglia were both brilliant, Tartaglia was relatively poor and self-taught, whereas Cardano had a job as a public lecturer and some connections with the upper class in Milan. Cardano knew he had an edge here, and he decided to use it to his advantage.
When the two finally met, Tartaglia was disappointed that Cardano had only a letter of introduction for him (he had hoped to be actually introduced). Nonetheless, the two talked, and eventually Tartaglia agreed to give Cardano his solution, as long as he promised to never publish it. Cardano agreed, and Tartaglia gave him the solution in the form of a poem, so that no one could decode it if it got into the wrong hands. I’m not sure why this was effective, though, since limericks aren’t exactly Morse code.
Cardano and his servant, Lodovico Ferrari (more on him in a minute) were able to come up with a pretty convincing proof for the solution of the cubic and even for the quartic, though Cardano did not publish these in order to keep his word to Tartaglia. Tartaglia, on the other hand, also did not publish his solution for six years, likely because he was saving them in case he got challenged again by a superior opponent. After all, no one else in the world could solve this problem except for him.
Four years after Cardano made his promise to Tartaglia, he heard that somewhere in Bologna, an Italian mathematician named Scipione del Ferro had independently solved the cubic equation. He and his servant Ferrari travelled to Bologna to meet the late mathematician’s son-in-law and found the solution in his notebook.
Cardano, figuring that he would not be breaking his promise since he could attribute the cubic’s solution to Ferro, published his own solutions. In the famous paper Ars Magna (The Great Art), he credited both Tartaglia and Ferro for their contributions. To this day, the Encyclopedia of Mathematics has named the cubic formula “Cardano’s formula”.
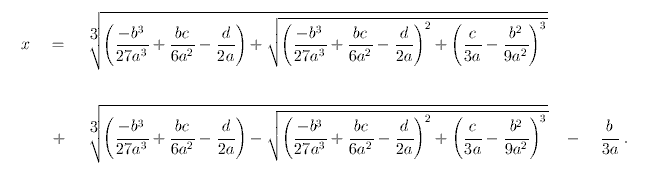
It is important to stop here and marvel at how revolutionary this single book was. In addition to containing the solution to cubic and the quartic equations, it is also the first recorded instance of a polynomial having multiple roots, and the first ever use of the complex numbers. So although Cardano took the solution to the cubic from Tartaglia and the solution to the quartic was taken from his student Ferrari, the book was monumental in its own right.
Tartaglia was enraged that Cardano (as he saw it) had broken his word. He tried to challenge Cardano, but instead Cardano just sent him pages of insults. The two argued for three years until in 1548, Tartaglia was offered a job as a lecturer in his birthplace of Brescia. In order to get the job, Tartaglia was asked to travel to Milan and challenge Cardano’s student, Lodovico Ferrari. You may be wondering how Ludovico Ferrari became a prominent mathematician when he was previously only mentioned as Cardano’s servant. Well, Ferrari’s life story is just as interesting as that of Cardano and Tartaglia.
Lodovico Ferrari
Lodovico Ferrari was born to a Milanese family that was forced to settle in Bologna during the Italian Wars. At some point Lodovico’s father was killed, and he was sent to live with his uncle Vincent (pretty much the premise of the Fresh Prince of Bel-Air, if you think about it). Lodovico’s belligerent cousin, Luke, ran away from home and began working for none other than Gerolamo Cardano, who was looking for a servant at the time. Luke wasn’t cut out for a job, however, so he ended up running away from Cardano and going back home to Milan. Enraged, Cardano sent a letter to Vincent Ferrari, requesting that his servant come back home. Vincent instead took this opportunity to keep his son at home and sent a fourteen year old Lodovico Ferrari to work in his place. Cardano figured he was better off with a more responsible servant and agreed.

Although Lodovico was originally meant to be a servant, Cardano soon discovered that the young boy was able to read and write. So Lodovico instead became a secretary. When it became clear that he was gifted in mathematics, Cardano began to teach him, and by the age of eighteen Lodovico Ferrari had a teaching job himself. In 1541, Cardan resigned from his lucrative teaching job, pitting Lodovico Ferrari against another mathematician for the job. As you would expect, the two held a math contest to decide who got the job, and Ferrari handily defeated his opponent, securing the distinguished job at the age of twenty. That’s younger than I am right now. Man, does that make me feel inadequate. Ferrari retired young at rich at 42 and lived the rest of his life in Bologna. Unfortunately, the rest of his life was only about a year, since he died of arsenic poisoning, which many believe to have been a murder attempt by his sisters.
Ferrari vs. Tartaglia
We skip back in time to 1548, when Tartaglia was asked to challenge a twenty-six year old Ferrari in order to secure a teaching job in Milan. The open letters between Tartaglia and Ferarri’s mentor Cardano were fairly scandalous at the time, and so a huge crowd (including many celebrities) attended the contest in Milan in the summer of 1548. The contest was such a big deal that the judge was the governor of Milan himself! For his entourage, the young Ferrari brought a large group of his friends and supporters. Tartaglia only brought his brother.
Tartaglia realized almost immediately that he was at a disadvantage, so he tried to cut off his opponent’s responses. Ferrari had a deep understanding of both the cubic and quartic equations (the latter of which was pretty much entirely his contribution to Cardano’s paper), and he trounced the Venetian veteran in the contest. Unwilling to accept his defeat, Tartaglia fled the contest, and Ferrari won by default.
Likely as a result of the contest, Tartaglia was not paid for his lecturing job and eventually got caught up in a vicious cycle of poverty and debt. He died penniless. On the other hand, Ferrari was offered a job from the emperor himself, and eventually ended up securing lucrative positions with the governor of Milan and at the church.
To Be Continued
This post ended up being longer than I expected, and we’ve only covered up to the solutions of the cubic and quartic equations. In the next part, I’ll be talking about the two mathematicians who finally solved the problem of the elusive quintic formula: the Norwegian Niels Henrik Abel, and the Frenchman Évariste Galois. Both of them found solutions independently (by fairly different methods) and the two men died within three years of each other. One died at 20; the other at 26. Stay tuned for tales about French Revolution and a tragically abridged love story in part two.
Share this on:
Recent Posts
- A Note on the Variation of Parameters Method | 11/01/17
- Group Theory, Part 3: Direct and Semidirect Products | 10/26/17
- Galois Theory, Part 1: The Fundamental Theorem of Galois Theory | 10/19/17
- Field Theory, Part 2: Splitting Fields; Algebraic Closure | 10/19/17
- Field Theory, Part 1: Basic Theory and Algebraic Extensions | 10/18/17